Рекурсивные функции вывода ряда Фибоначчи и вычисления факториала

Что такое числа Фибоначчи и факториал, а также как решаются задачи их вычисления на Python с помощью циклов проиллюстрировано здесь и здесь. В данной статье будет показано, как эти задачи могут быть решены с помощью рекурсии, то есть определения рекурсивных функций.

В программировании рекурсия — это вызов функции из нее же самой (в простейшем случае). Обычно рекурсией заменяют цикл, хотя эффективность такой замены может быть сомнительной. В теле рекурсивной функции должно быть условие, при котором вызовы из тела функции самой себя будут прекращены.

Рекурсивное вычисление n-го числа ряда Фибоначчи

Если переменная n равна 1 или 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
Во всех остальных случаях вызвать эту же функцию с аргументами n - 1 и n - 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.

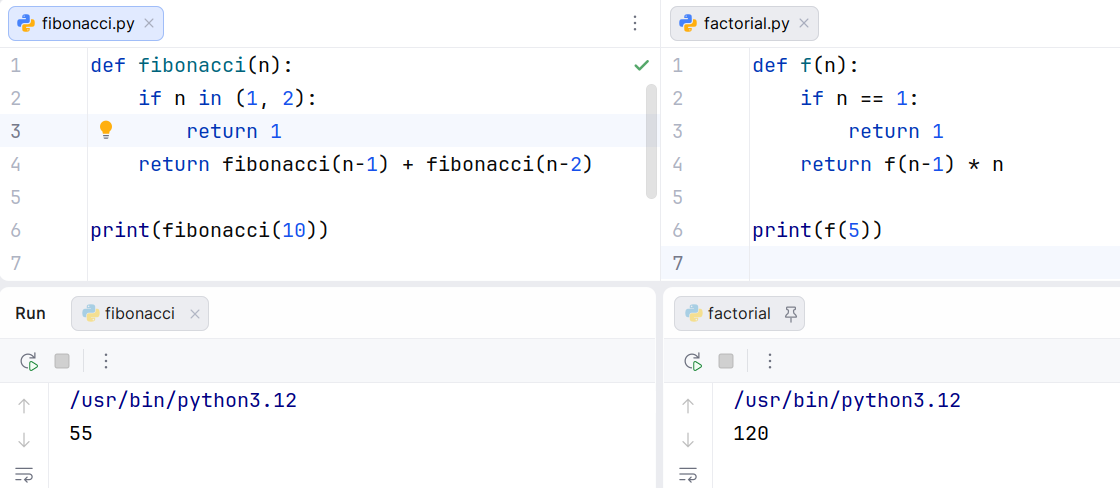
def fibonacci(n):
    if n in (1, 2):
        return 1
    return fibonacci(n-1) + fibonacci(n-2)


print(fibonacci(10))

Рассмотрим стек вызовов n = 4. Тогда произойдет рекурсивный вызов fibonacci(3) и fibonacci(2). Второй вернет единицу, а первый приведет к еще двум вызовам функции: fibonacci(2) и fibonacci(1). Оба вызова вернут единицу, в сумме будет два. Таким образом, вызов fibonacci(3) возвращает число 2, которое суммируется с числом 1 от вызова fibonacci(2). Результат 3 возвращается в основную ветку программы. Четвертый элемент ряда Фибоначчи равен трем: 1 1 2 3.

Нахождение факториала рекурсией

def f(n):
    if n == 1:
        return 1
    return f(n-1) * n

print(f(5))

Поток выполнения программы при n = 5:

Вызов функции f(5)
f(5) вызывает f(4)
f(4) вызывает f(3)
f(3) вызывает f(2)
f(2) вызывает f(1)
f(1) возвращает в f(2) число 1
f(2) возвращает в f(3) число 1 * 2, т. е. 2
f(3) возвращает в f(4) число 2 * 3, т. е. 6
f(4) возвращает в f(5) число 6 * 4, т. е. 24
f(5) возвращает число 24 * 5, т. е. 120 в основную ветку программы
Число 120 выводится на экран