Заполнение списка положительными и отрицательными случайными числами (без нуля)

Заполнить список отрицательными и положительными случайными числами. При этом в списке не должно быть нулей.

Количество элементов в списке: 10
Диапазон отрицательных чисел: [-5, -1]
Диапазон положительных чисел: [1, 5]

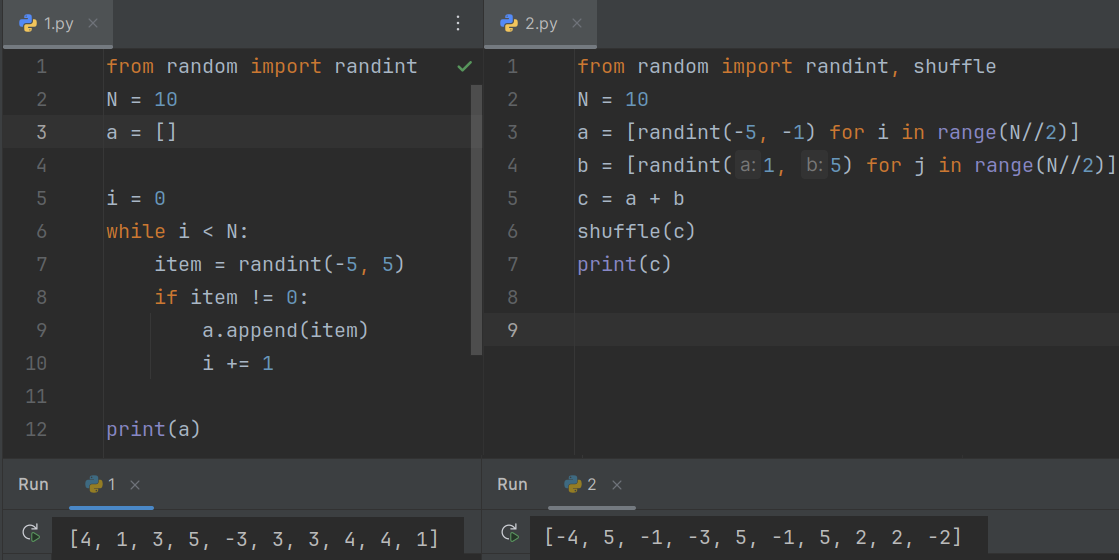
Решение задачи на языке программирования Python

В более обобщенном виде это задача на заполнение случайными числами с любым разрывом диапазона.

Задача осложняется тем, что если задать единый диапазон от -5 до 5 для генерации случайных чисел, то в нем могут также оказаться нули в неизвестных нам количестве. Если потом их удалить из списка, в нем останется уже не 10 элементов.

"Прямолинейный" вариант решения данной задачи - это перед добавлением элемента проверять его значение на неравенство нулю, а также ввести счетчик добавленных в список элементов. Таким образом генерация случайных чисел будет продолжаться, пока список не заполнится требуемым количеством значений.

from random import randint
N = 10
a = []

i = 0
while i < N:
    item = randint(-5, 5)
    if item != 0:
        a.append(item)
        i += 1

print(a)

Пример результата:

[4, -2, -3, 5, 3, 4, -3, 3, 4, 1]

Другой способ решения - сначала заполнить один список отрицательными числами, второй - положительными. Потом списки объединить и перемешать их значения с помощью метода shuffle модуля random.

from random import randint, shuffle
N = 10
a = [randint(-5, -1) for i in range(N//2)]
b = [randint(1, 5) for j in range(N//2)]
c = a + b
shuffle(c)
print(c)

Если количество элементов нечетное, то один элемент можно потом удалить по случайному индексу:

from random import randint, shuffle
N = 11
a = [randint(-5, -1) for i in range((N+1)//2)]
b = [randint(1, 5) for j in range((N+1)//2)]
c = a + b
shuffle(c)
del c[randint(0, N)]
print(c)

Пример результата:

[3, -5, -3, 3, 2, -4, 4, -1, -4, 5, 1]

Однако второе (и третье) решение не идентичны по смыслу первому, где список заполняется в одном общем цикле. В первом случае список "более случайный". Мы не можем заранее сказать, сколько в нем будет положительных, а сколько отрицательных чисел. Одних может быть больше, чем других. В случае решения через объединение в списке будет равное количество положительных и отрицательных чисел (или каких-то больше на 1, если количество элементов нечетное).

Больше задач в PDF