Решето Эратосфена — алгоритм определения простых чисел
Решето Эратосфена — это алгоритм нахождения всех простых чисел до заданного натурального числа путем постепенного отсеивания составных чисел. Образно говоря, через решето Эратосфена в процессе его тряски проскакивают составные числа, а простые остаются в решете.
Чтобы понять данный алгоритм, вспомним, что числа являются простыми, если делятся только на единицу и самих себя. Первое простое число — это 2, второе простое число — это 3. Теперь начнем рассуждать:
- Все четные числа, кроме двойки, — составные, т.е. не являются простыми, так как делятся не только на себя и единицу, а также на 2.
- Все числа кратные трем, кроме самой тройки, — составные, так как делятся не только на самих себя и единицу, а также еще на 3.
- Число 4 уже выбыло из игры, так как делится на 2.
- Число 5 простое, так как его не делит ни один простой делитель, стоящий до него.
- Если число не делится ни на одно простое число, стоящее до него, значит оно не будет делиться ни на одно сложное число, стоящее до него.
Последний пункт вытекает из того, что сложные числа всегда можно представить как произведение простых. Поэтому если одно сложное число делится на другое сложное, то первое должно делиться на делители второго. Например, 12 делится на 6, делителями которого являются 2 и 3. Число 12 делится и на 2, и на 3.
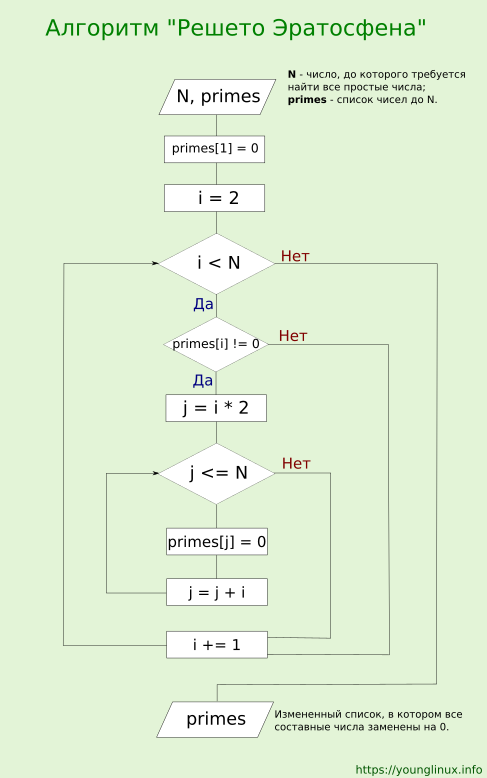
Алгоритм Эратосфена как раз заключается в последовательной проверке делимости чисел на предстоящие простые числа. Сначала берется первое простое и из ряда натуральных чисел высеиваются все кратные ему. Затем берется следующее простое и отсеиваются все кратные ему и так далее.
При реализации алгоритма Эратосфена на языке программирования есть некоторая сложность. Допустим, мы помещаем натуральные числа до заданного числа N в массив. Далее в процессе выполнения алгоритма будем заменять обнаруженные сложные числа нулями. После выполнения алгоритма те ячейки массива, которые не содержат нули, содержат простые числа, которые выводятся на экран.
Однако индексация массива начинается с нуля, а простые числа начинаются с двойки. Эта проблема решаема, но добавляет сложности в код. Поскольку алгоритм Эратосфена не такой уж простой, легче пренебречь началом и взять массив от 0 до N. Здесь важнее индексы, чем значения элементов. Значениями могут быть логические True, обозначающее простое число, и False, обозначающее сложное число.
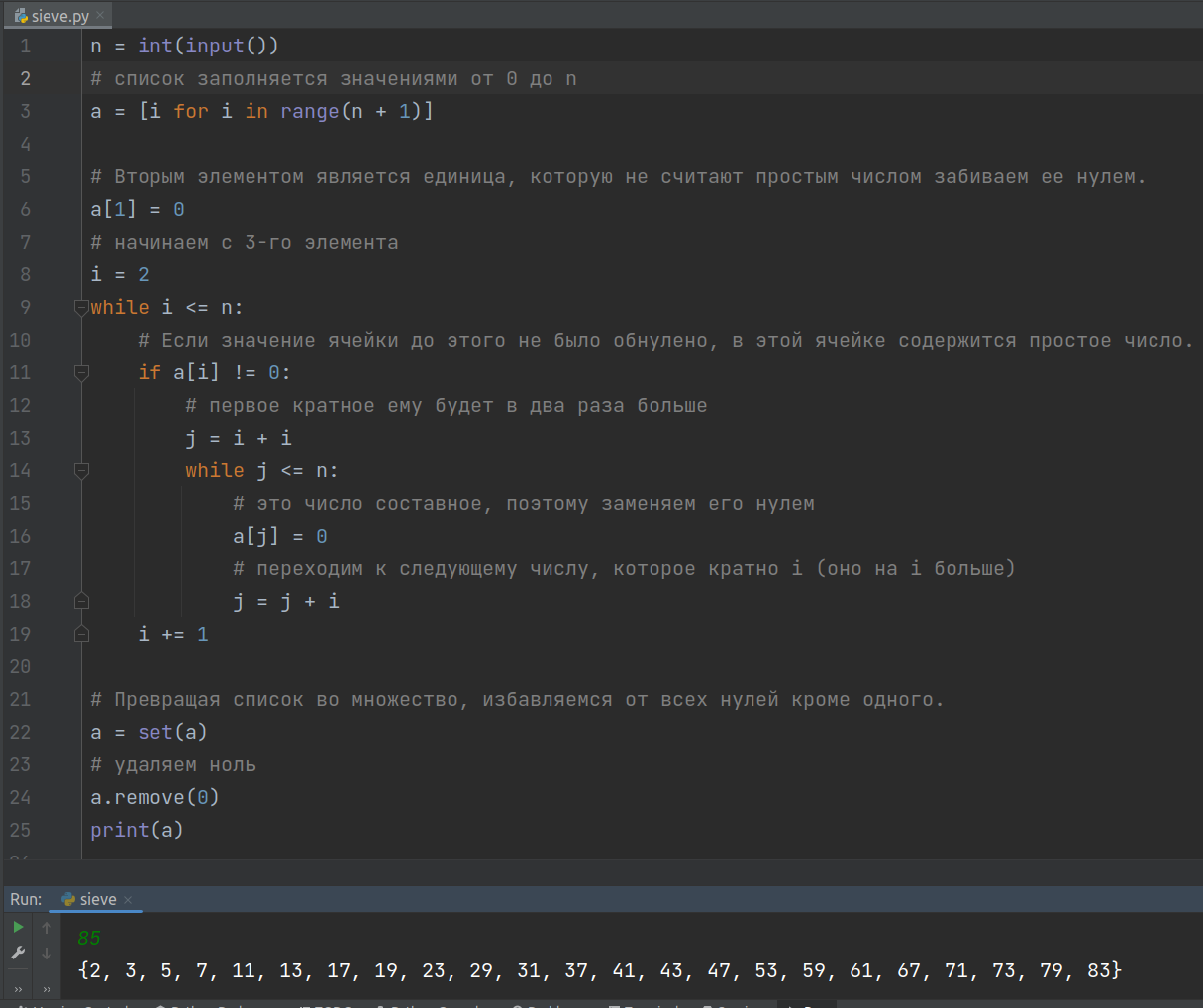
В данном примере реализации алгоритма Эратосфена на языке программирования Python список заполняется числами от 0 до N включительно так, что индексы элементов совпадают с их значениями. Далее все непростые числа заменяются нулями:
N = int(input()) # Создается список из значений от 0 до N включительно primes = [i for i in range(N + 1)] # Вторым элементом списка является единица, которую # не считают простым числом. Забиваем ее нулем primes[1] = 0 # Начинаем с 3-го элемента i = 2 while i <= N: # Если значение текущей ячейки до этого не было обнулено, # значит в этой ячейке содержится простое число if primes[i] != 0: # Первое кратное ему будет в два раза больше j = i + i while j <= N: # и это число составное, # поэтому заменяем его нулем primes[j] = 0 # переходим к следующему числу, # которое кратно i (оно на i больше) j = j + i i += 1 # Избавляемся от всех нулей в списке primes = [i for i in primes if i != 0] print(primes)
Пример выполнения:
35 [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]