Перевод десятичного числа в любую систему счисления
Написать программу, которая переводит десятичное число в любую другую систему счисления. Десятичное число и основание новой системы счисления вводятся с клавиатуры. При желании реализовать в программе функцию такого преобразования.
Решение задачи на языке программирования Python
Алгоритм перевода десятичного числа в любую другую систему счисления заключается в последовательном целочисленном делении сначала самого десятичного числа, а потом получаемых частных на основание системы счисления, в которую переводится число. Из остатков такого деления собирается представление числа в новой системе счисления. В той, на основание которой происходило деление. Сбор остатков происходит с конца.
Например, перевод десятичных чисел 160 в восьмеричную и 18 в двоичную системы счисления будет выглядеть так:
160 / 8 = 20 | 0 20 / 8 = 2 | 4 2 / 8 = 0 | 216010 = 2408 |
18 / 2 = 9 | 0 9 / 2 = 4 | 1 4 / 2 = 2 | 0 2 / 2 = 1 | 0 1 / 2 = 0 | 11810 = 100102 |
Даже если использовать этот алгоритм для перевода десятичного числа в десятичную систему счисления будет получен верный результат.
150 // 10 = 15 | 0 15 // 10 = 1 | 5 1 // 10 = 0 | 115010 = 15010
Проблема появляется в тот момент, когда основание системы счисления начинает превышать 10. В таких случаях нам не хватает привычных символов цифр (0–9) и требуется ввод дополнительных символов для обозначения значений, соответствующих десятичным числам 10, 11, 12 и т. д. Для примера переведем десятичное число в шестнадцатеричную систему счисления:
700 // 16 = 43 | 12 (C) 43 // 16 = 2 | 11 (B) 2 // 16 = 0 | 270010 = 2BC16
Десятичные остатки 12 и 11 при формировании шестнадцатеричного числа должны быть представлены одним разрядом. В таких случаях в качестве цифр, чье значение больше 9-ти, используются английские буквы. Так числу 10 будет соответствовать символ A, числу 11 — B и т. д.
Таким образом, при написании программы перевода десятичного числа в любую систему счисления мы должны предусмотреть подмену остатков на соответствующие им символы, если эта замена требуется.
Будем усложнять программу поэтапно и сначала напишем вариант кода, который переводит не в любую систему счисления, а только с основанием до 10-ти.
num = int(input()) base = 0 while not (2 <= base <= 9): base = int(input('Основание (2-9): ')) new = '' while num > 0: remainder = num % base new = str(remainder) + new num = num // base print(new)
В цикле сначала вычисляется остаток. Далее присоединяем его спереди к строковой переменной new, в которой хранится представление числа в новой системе счисления. Последним действием присваиваем переменной num частное от целочисленного деления прежнего значения num на основание системы счисления.
Пример выполнения:
160 Основание (2-9): 8 240
Поскольку в языке программирования Python есть функция divmod, сократим код, объединив нахождение остатка и целочисленное деление:
... while num > 0: num, remainder = divmod(num, base) new = str(remainder) + new ...
Вызов divmod(num, base) возвращает кортеж из частного и остатка от деления num на base. Далее частное присваивается num, остаток - remainder.
Теперь напишем программу, которая переводит число исключительно в шестнадцатеричную систему счисления. Для хранения символов, которыми будут заменяться двузначные остатки, используем строку из этих символов.
num = int(input()) base = 16 letters = 'ABCDEF' new = '' while num > 0: num, remainder = divmod(num, base) if remainder > 9: letter_id = remainder - 10 remainder = letters[letter_id] new = str(remainder) + new print(new)
Числу 10 соответствует символ A. Поэтому если остаток равен десяти, то letter_id будет равно нулю. Символ под индексом 0 в строке букв — как раз A. Если остаток равен 15-ти, то letter_id будет равно пяти, а letters[5] вернет F.
Программу можно упростить, если в строку символов добавить цифры. В этом случае остатки будут точно соответствовать индексам, под которыми находятся соответствующие им символы.
num = int(input()) base = 16 letters = '0123456789ABCDEF' new = '' while num > 0: num, remainder = divmod(num, base) new = letters[remainder] + new print(new)
На этом этапе должно стать понятно, как написать программу конвертации десятичного числа в почти любую систему счисления. Достаточно немного подправить код перевода в шестнадцатеричную систему, дописав в строку дополнительный набор символов, а не заканчивать ее на F.
Чтобы не хранить в программе строку большой длины и избежать ошибки из-за нечаянно пропущенного какого-нибудь символа, вернемся к варианту, в котором остатки больше девяти заменяются в теле условного оператора. При этом буквы будем брать не из определенной в коде строки, а из встроенной таблицы символов.
num = int(input()) base = 0 while not (2 <= base <= 36): base = int(input('Основание (2-36): ')) new = '' while num > 0: num, remainder = divmod(num, base) if remainder > 9: letter = remainder - 10 remainder = chr(ord('A') + letter) new = str(remainder) + new print(new)
Вызов ord('A') возвращает код буквы A в таблице Unicode. К этому коду-числу мы прибавляем смещение по алфавиту (значение letter). С помощью функции chr() получаем соответствующую коду букву.
В виде функции:
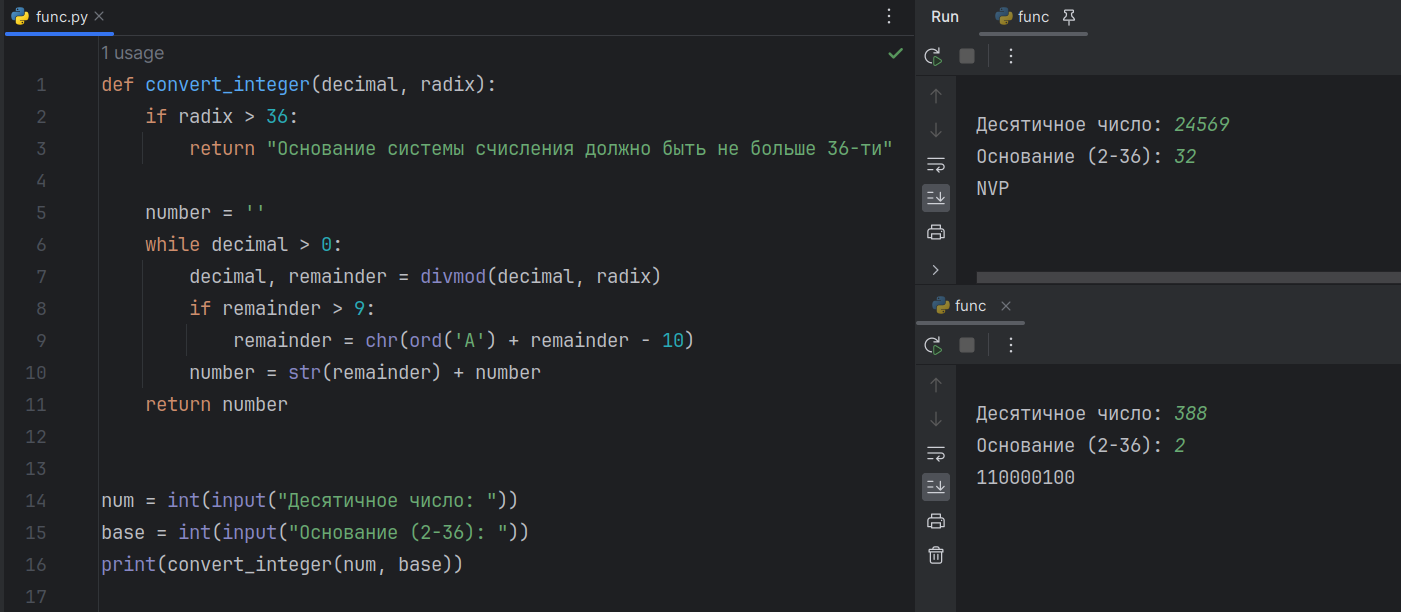
def convert_integer(decimal, radix): if radix > 36: return 'Основание системы счисления должно быть не больше 36-ти' number = '' while decimal > 0: decimal, remainder = divmod(decimal, radix) if remainder > 9: remainder = chr(ord('A') + remainder - 10) number = str(remainder) + number return number num = int(input('Десятичное число: ')) base = int(input('Основание (2-36): ')) print(convert_integer(num, base))
Десятичное число: 1750 Основание (2-36): 36 1CM
Ограничение по основанию в 36 связано с количеством букв в английском алфавите. Их 26, плюс десять цифр. Расширить диапазон оснований можно за счет взятия недостающих символов из какой-либо другой части таблицы Unicode. Например, можно добавить к условному оператору ветку elif с условием remainder > 35, а в теле из remainder вычитать 36.
Однако написать программу, которая переводит десятичное число в абсолютно любую систему счисления нельзя. Иначе надо суметь решить задачу генерации случайного символа, который не должен быть похож ни на какой из полученных ранее.