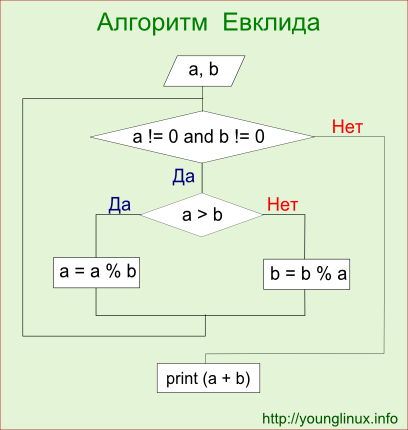
Алгоритм Евклида - нахождение наибольшего общего делителя

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа.

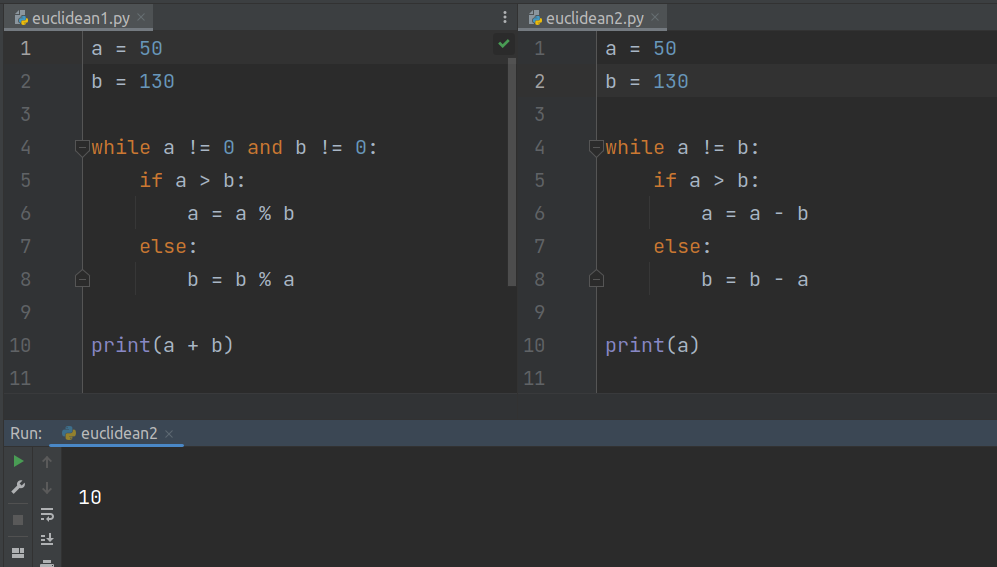
Решение задачи на языке программирования Python

Алгоритм нахождения НОД делением

1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6

a = int(input())
b = int(input())

while a != 0 and b != 0:
    if a > b:
        a = a % b
    else:
        b = b % a

print(a + b)

В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для определения НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Если условием завершения цикла является равенство хотя бы одной из переменных нулю (a == 0 or b == 0), то условием продолжения его работы является обратное этому условие - обе переменные должны иметь отличные от нуля значения (a != 0 and b != 0).

Для того чтобы вышеприведенная программа могла обрабатывать отрицательные числа, в логическом выражении при if должны сравниваться модули значений переменных: if abs(a) > abs(b):. Иначе большим числом может оказаться меньшее по модулю. В этом случае интерпретатор Питона в качестве остатка от деления выдает вещественное число. В результате это приводит к зацикливанию, так как низвести переменные до нуля становится как минимум маловероятным.

Алгоритм нахождения НОД вычитанием

1. Из большего числа вычитаем меньшее.
2. Если получается 0, значит, числа равны друг другу и являются НОД (следует выйти из цикла).
3. Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 - 18 = 12
18 - 12 = 6
12 - 6 = 6
6 - 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6

a = int(input())
b = int(input())

while a != b:
    if a > b:
        a = a - b
    else:
        b = b - a

print(a)

Функция, вычисляющая НОД

def gcd(m, n):
    while m != n:
        if m > n:
            m = m - n
        else:
            n = n - m
    return n


a = int(input())
b = int(input())

print(gcd(a, b))

Функция gcd модуля math

В модуле math языка программирования Python есть функция gcd, вычисляющая наибольший общий делитель двух чисел.

>>> import math
>>> math.gcd(30, 18)
6

Больше задач в PDF