Проверка простоты числа перебором делителей

Решение задачи на языке программирования Python

Простые числа - это натуральные числа больше единицы, которые делятся нацело только на единицу и на себя. Например, число 3 простое, так как нацело делится только на 1 и 3. Число 4 сложное, так как нацело делится не только на 1 и 4, но также на число 2.

Алгоритм перебора делителей заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню из тестируемого числа. Таким образом, в данном алгоритме используется цикл, счетчик итераций которого последовательно принимает значения ряда натуральных чисел от 2 до корня из исследуемого числа.

Перебор делителей применяется в том числе для определения, является ли натуральное число простым, или оно является сложным, то есть составным. Касаемо данной задачи, если хотя бы один делитель делит исследуемое число без остатка, то оно является составным. Если ни одного такого делителя не находится, то число признается простым.

from math import sqrt

n = int(input())

prime = True

i = 2
while i <= sqrt(n):
    if n % i == 0:
        prime = False
        break
    i += 1

if prime:
    print('Простое число')
else:
    print('Составное число')

В программе мы сначала предполагаем, что введенное число n является простым, и поэтому присваиваем переменной prime значение True. Далее в цикле перебираются делители (переменная i ) от 2-х до квадратного корня из числа n. Как только встречается первый делитель, на который n делится без остатка, меняем значение prime на False и прерываем работу цикла, так как дальнейшее тестирование числа на простоту смысла не имеет.

Если после выполнения цикла prime осталась истиной, сработает ветка if условного оператора. В случае False, поток выполнения заходит в ветку else.

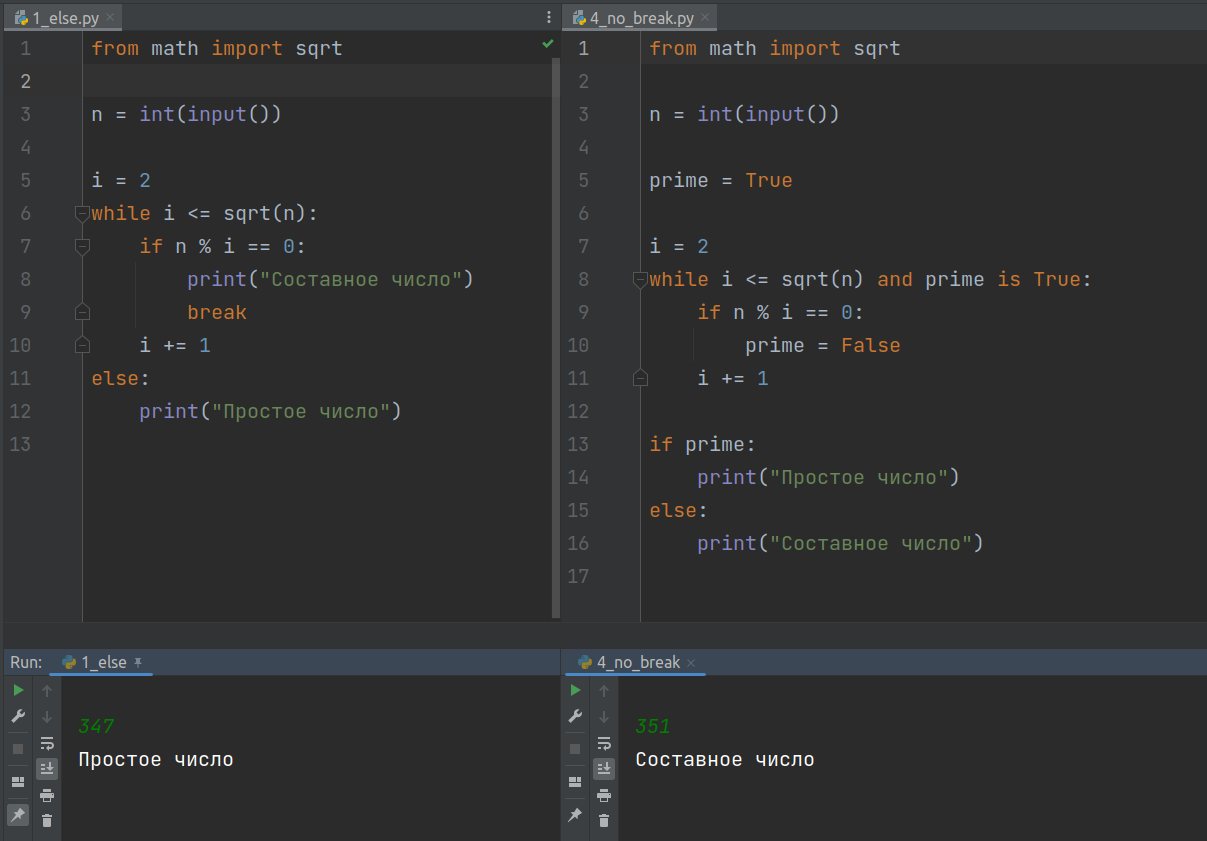
Если знать о такой особенности циклов в Python как возможность иметь ветку else, то код можно упростить, избавившись от переменной prime и ее проверки условным оператором после завершения работы цикла.

from math import sqrt

n = int(input())

i = 2
while i <= sqrt(n):
    if n % i == 0:
        print('Составное число')
        break
    i += 1
else:
    print('Простое число')

Ветка else при циклах (как while, так и for) срабатывает, если в основном теле цикла не происходило прерывания с помощью break. Если break сработал, то тело else выполняться не будет. При использовании таких конструкций также следует помнить, что если условие в заголовке цикла сразу возвращает ложь (то есть тело цикла не должно выполняться ни разу), код тела else все-равно будет выполнен.

Программы выше будут определять числа 0 и 1 как простые. Это неправильно. Данные числа не являются ни простыми, ни сложными. Для проверки ввода пользователя, можно воспользоваться условным оператором или зациклить запрос числа, пока не будет введено корректное значение:

n = 0
while n < 2:
    n = int(input())

Рассмотрим функцию, которая определяет, является ли число простым:

from math import sqrt


def is_prime(n):
    i = 2
    while i <= sqrt(n):
        if n % i == 0:
            return False
        i += 1
    if n > 1:
        return True


a = int(input())

if is_prime(a):
    print('Простое число')
else:
    print('Число НЕ является простым')

Здесь нет необходимости в прерывании работы цикла с помощью break, так как оператор return выполняет выход из тела всей функции.

Если цикл полностью отработал, выполнится выражение return True, находящееся ниже цикла. Оно помещено в тело условного оператора, чтобы исключить возврат "истины", когда в функцию передаются числа 0 или 1. В этом случае функция вернет объект None.

Программа не защищена от ввода отрицательного числа. При этом будет генерироваться ошибка на этапе извлечения квадратного корня.

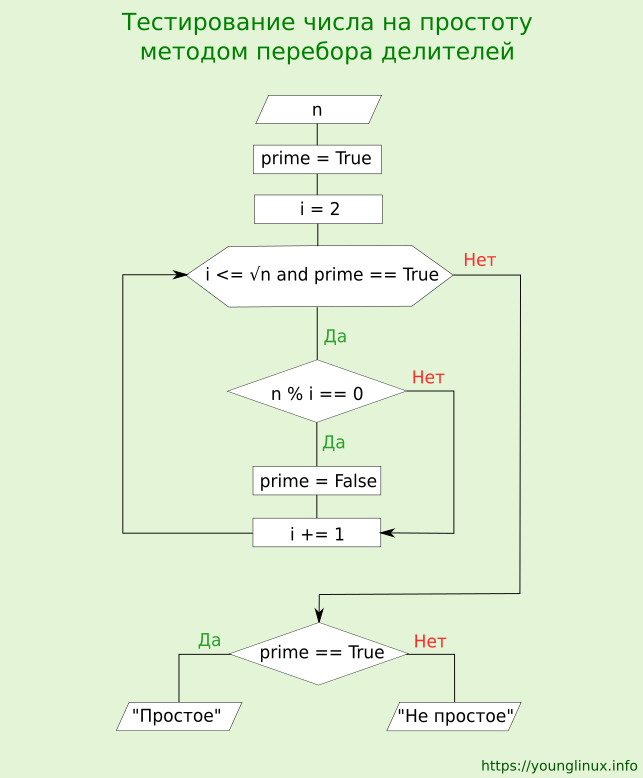
Нарисуем блок-схему тестирования числа на простоту (без дополнительных проверок и оператора break):

from math import sqrt

n = int(input())

prime = True

i = 2
while i <= sqrt(n) and prime is True:
    if n % i == 0:
        prime = False
    i += 1

if prime:
    print('Простое число')
else:
    print('Составное число')

Больше задач в PDF