Арифметические операции с массивами в NumPy. Вывод графиков по формуле

Создано: 18.11.2025

В NumPy экземпляры ndarray одинаковой размерности можно между собой складывать, вычитать, умножать и делить. Эти действия можно назвать базовыми операциями.

a = np.array([12, -8, 4, 0])
b = np.array([0.12, 0.34, 0.56, 0.81])
print(a + b)
print(a - b)
print(a * b)
print(a / b)

[12.12 -7.66  4.56  0.81]
[11.88 -8.34  3.44 -0.81]
[ 1.44 -2.72  2.24  0.  ]
[100.         -23.52941176   7.14285714   0.        ]

В результате их выполнения создается новый массив, значение каждого элемента которого — это сумма, разность, произведение или частное от значений элементов исходных массивов, находящихся в такой же позиции. То есть операции выполняются поэлементно.

Кроме этого, массивы NumPy можно изменять на скалярную величину. В этом случае каждое значение исходного массива умножается, складывается, возводится в степень и т.п. на/в одну и ту же величину.

a = np.array([12, -8, 3, 0])
print(a + 3)    # [15 -5  6  3]
print(a - 1)    # [11 -9  2 -1]
print(a * 1.2)  # [14.4 -9.6  3.6  0. ]
print(a // 2)   # [ 6 -4  1  0]
print(a / 2)    # [ 6.  -4.   1.5  0. ]
print(a ** 2)   # [144  64   9   0]

Возможны и обратные действия, когда скаляр стоит первым операндом, а массив — вторым. Так в примере выше выражение 1 - a дало бы массив [-11, 9, -2, 1].

Далее кажется естественным предположить, что в библиотеке NumPy должны быть функции, позволяющие выполнять с объектами ndarray другие операции, которые не задаются операндами–символами. И таковые действительно есть, они называются универсальными функциями (класс ufunc). Например, мы не можем использовать функцию sqrt из модуля math языка Python. Однако аналогичная есть в NumPy и предназначена для работы с массивами.

a = np.array([12, 8, 3, 0])
b = np.sqrt(a)
print(np.round(b, 2))

[3.46 2.83 1.73 0.  ]

Кроме извлечения квадратного корня и округления в NumPy есть множество других, среди которых тригонометрические, для поиска минимума, максимума, сортировки, суммирования значений одного массива. Какие-то из них мы используем позже в другом контексте.

Сейчас обратим внимание на то, что базовые операции с массивами и ряд универсальных функций позволяют легко строить графики функций, в которых одна координата вычисляется по формуле и зависит от значения другой. Это избавляет от необходимости хранить в программе два экземпляра ndarray. В функцию plot библиотеки Matplotlib мы можем передавать один массив и формулу. Второй массив будет генерироваться только в момент его использования.

import numpy as np
import matplotlib.pyplot as plt

a = np.arange(0, 100)
plt.plot(a, np.sqrt(a))
plt.plot(a, 2 + np.sin(a*3))

b = np.linspace(0, 100, 10)
plt.plot(b, 7 + b * 0, 'o:r')
plt.annotate('Значение Y одинаково,\nточки на отрезке',
             xy=(0, 7.3), color='r')
plt.show()

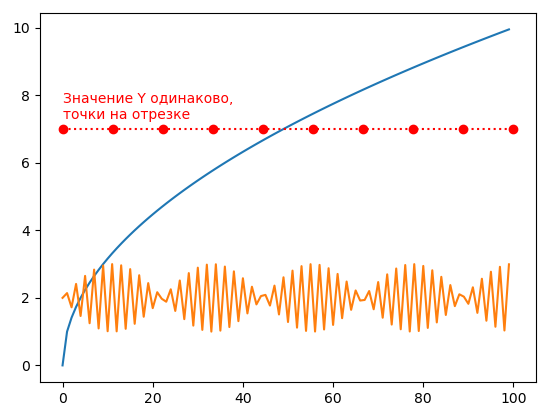
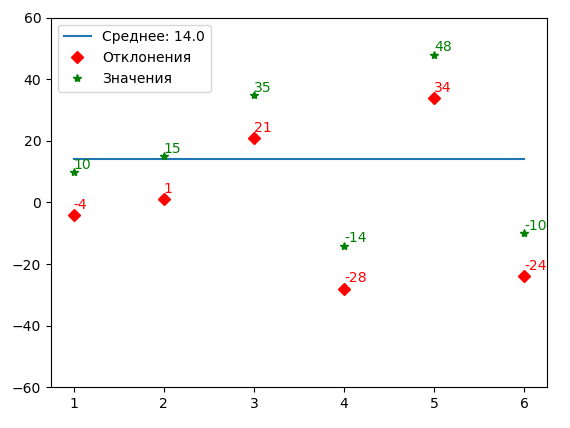
Не все универсальные функции возвращают массив. Вместо этого они дают одно число. Так в примере ниже average() возвращает среднее значение для элементов массива. Мы можем использовать это число не само по себе, а в формуле получения другого массива (некого отклонения).

import numpy as np
import matplotlib.pyplot as plt

b = np.array([10, 15, 35, -14, 48, -10])
avr = np.average(b)  # среднее
c = b - avr  # отклонения
c = c.astype(int)

plt.ylim(-60, 60)  # установка пределов для оси Y
plt.plot([1, len(b)], [avr, avr], label=f'Среднее: {avr}')
plt.plot(np.arange(1, len(b)+1), c, 'Dr', label='Отклонения')
plt.plot(np.arange(1, len(b)+1), b, '*g', label='Значения')
plt.legend()

for i, j in zip(np.arange(1, len(b)+1), c):
    plt.text(i, j+2, str(j), color='r')

for i, j in zip(np.arange(1, len(b)+1), b):
    plt.text(i, j+1, str(j), color='g')

plt.show()

Если последовательность точек не важна, то есть мы не строим график функции, то можно использовать диаграммы рассеяния (строятся вызовом функции scatter() модуля pyplot). Примерно ту же самую картину можно получить так:

plt.plot([1, len(b)], [avr, avr], label=f'Среднее: {avr}')
plt.scatter(np.arange(1, len(b)+1), c, marker='D', label='Отклонения')
plt.scatter(np.arange(1, len(b)+1), b, label='Значения')

Среди множества настроек диаграмм рассеяния имеется возможность задавать свой размер для каждой точки.