Фильтрация массивов в NumPy

Создано: 28.12.2025

В NumPy не получится в цикле добавлять "прошедшие проверку" элементы массива в другой, то есть осуществлять выбор по условию, так как размер экземпляров ndarray менять нельзя. Мы можем использовать функцию filter самого языка Python. Однако, чтобы получить массив отфильтрованных значений, полученный из filter объект сначала должен быть преобразовать в список, потом — в ndarray. Поэтому в NumPy используется другой принцип.

Если в квадратных скобках после имени переменной, связанной с объектом ndarray, указать список или массив, состоящий из значений True и False и имеющий такую же длину, то он послужит так называемой булевой маской (boolean index list). Это значит, что если в определенной позиции маски стоит True, то элемент исходного массива попадает в новый.

import numpy as np

a = np.array(['apple', 'banana', 'orange', 'tomato', 'potato'])

mask1 = [True, True, False, True, False]
b = a[mask1]
print(b)  # ['apple' 'banana' 'tomato']

c = a[[True, False, False, False, True]]
print(c)  # ['apple' 'potato']

mask3 = np.random.choice([True, False], size=5, p=(0.75, 0.25))
d = a[mask3]
print(d)

Вручную составлять булевы маски — утомительное занятие. Однако то, что маской может быть список, а не массив, позволяет нам в цикле создавать саму маску, добавляя в нее True, если элемент массива соответствует условию выбора, и False — если нет.

a = np.random.normal(scale=5, size=10).astype('i2')
print(a)

mask = []
for i in a:
    if i >= 0:
        mask.append(True)
    else:
        mask.append(False)

print(a[mask])

[ 4 -1 -1  0  3  3 -3  0 -3  5]
[4 0 3 3 0 5]

На самом деле в NumPy делать так нет необходимости, так как применение булевой операции к экземпляру ndarray возвращает массив, состоящий из True и False, то есть по-сути — булеву маску. Это есть следствие поэлементного применения операции, как это было бы в случае с арифметической операцией массива со скалярной величиной.

a = np.random.normal(scale=5, size=5).astype('i2')
print(a)

mask = a >= 0
print(mask)

print(a[mask])

[  0  -6   2 -11   1]
[ True False  True False  True]
[0 2 1]

В результате при фильтрации массивов в NumPy нередко можно видеть сокращенный синтаксис, когда логическое выражение помещается в квадратные скобки при имени массива. На самом деле за таким синтаксисом скрыто два действия — получение массива-маски, ее применение для получения отфильтрованных значений:

a = np.random.normal(scale=10, size=10).astype('i2')
print(a)

print(a[a >= 0])
print(a[a % 2 == 0])
print(a[(a > 5) | (a < -3)])

[-11   5 -16  -3   0  -6   4  17   8  -2]
[ 5  0  4 17  8]
[-16   0  -6   4   8  -2]
[-11 -16  -6  17   8]

Обратите внимание, что в сложных логических выражениях с массивами используются свои логические операторы (| вместо or, & вместо and).

Рассмотрим как на практике может применяться фильтрация массивов в NumPy. Пусть необходимо из распределения удалить все выбросы. Ими будем считать значения, уходящие за полтора межквартильного размаха от начала 0.25-го квартиля в левую сторону и на такое же расстояние от конца 0.75-го квартиля в правую (см. предыдущий урок).

В NumPy есть функция quantile, которая возвращает значение-границу переданного в нее квантиля. В качестве примечания заметим, что квартили являются частными случаями квантилей. Они делят массив на 4 равные части, но его можно делить на любое количество частей.

import numpy as np
import matplotlib.pyplot as plt

a = np.random.normal(scale=10, size=100).astype('i2')

q1 = np.quantile(a, 0.25)
q3 = np.quantile(a, 0.75)
left_fliers = q1 - 1.5 * (q3 - q1)
right_fliers = q3 + 1.5 * (q3 - q1)

a_without_fliers = a[(a >= left_fliers) & (a <= right_fliers)]
a_fliers = a[(a < left_fliers) | (a > right_fliers)]

plt.title(f'Box: {q1}, {q3}. '
          f'Whisker limits: {left_fliers}, {right_fliers}
'
          f'Fliers: {a_fliers}')
data = [a, a_without_fliers]
plt.boxplot(data)
plt.grid(axis='y')
plt.yticks(np.arange(-30, 30, 5))
plt.show()

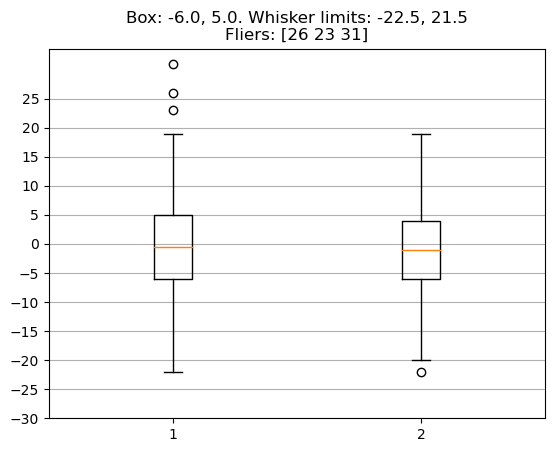
Обратите внимание, что если границы ящика на левой диаграмме совпадают с найденными значениями для q1 и q3, то границы усов — нет. Это связано с тем, что на графике отображаются реально существующие значения массива, а не сами границы. То есть, если у нас верхняя граница равна 21.5, а в отсортированном варианте массива за числом 19 будет стоять число 23, то на боксплоте граница уса будет соответствовать числу 19.

Во вторых, правый боксплот на основе уже "очищенных" данных может немного отличаться от построенного по исходным, так как удаленные выбросы могли вносить свой вклад в характеристики распределения.