Распределения в NumPy, их визуализация с помощью Matplotlib и Seaborn
Создано: 10.12.2025
В статистике, перед тем как данные анализировать, их надо собрать. Например, это может быть выборка о том, сколько каждый входящий в нее человек спит в сутки. Или высота каждого растения на грядке. Или суточный срез количества времени, которое каждый посетитель провел на сайте. Другими словами, данные могут быть разного рода, и это нас сейчас не интересует.
Важен сам факт того, что у нас есть массив, каждое значение в котором несет информацию о величине одного и того же признака разных экземпляров, то есть имеется статистика.
Когда начинают анализировать такую статистику, то выясняют, какие значения или пределы значений в ней встречаются чаще всего, а какие — реже, то есть определяют распределение вероятностей значений признака.
Часто встречающимся вариантом является нормальное распределение. Если на его основе построить график, то он будет иметь вид колоколообразной кривой, потому что экземпляров с более близким к среднему значению признака будет больше всего. И чем дальше от среднего, тем их будет меньше.
Когда собранных статистических данных нет, но есть необходимость имитировать определенное распределение (для симуляции, машинного обучения и др.), используют ряд методов из модуля random библиотеки NumPy. Так для получения нормального распределения предназначена функция normal.
Все аргументы normal() являются необязательными, при этом size — размер выборки (сколько будет чисел в массиве), loc — среднее значение, scale — стандартное отклонение (разброс данных; чем меньше, тем данные "плотнее").
import numpy as np import matplotlib.pyplot as plt fig, axes = plt.subplots(1, 2, figsize=(10, 4)) a = np.random.normal(size=100) print(a[0]) # вещественное число, например, 0.3978873303332952 axes[0].plot(a, marker='.', linewidth=0.5) b = np.random.normal(size=50, loc=10, scale=5) axes[1].plot(b, marker='*', linewidth=0.5, color='y') plt.show()
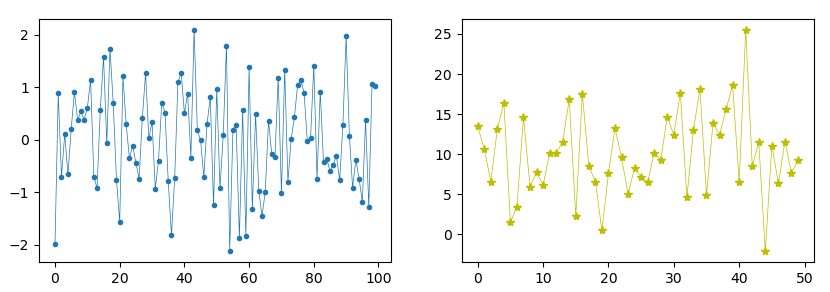
По умолчанию loc равен нулю, а scale единице (стандартное отклонение — это не разница между минимум и максимумом, оно вычисляется по особой формуле). В результате на первом графике мы видим, что больше всего значений массива находятся ближе к нулю.
Сказать по таким графикам, что перед нами действительно нормальное распределение, весьма сложно. Представьте, что у вас реальные данные исследования и вы не знаете, какое тут распределение. Чтобы подтвердить его нормальность, надо посчитать сколько измерений (элементов массива) имеют одно значение, сколько — другое и так далее. После этого построить диаграмму, где по оси x будет значение признака, а по оси y — количество элементов в массиве с таким значением. Если такой график или диаграмма будут иметь вид колокола, то перед нами нормальное распределение.
Однако функция normal() возвращает вещественные числа, и каждое из них уникально, повторения очень редки. Чтобы избавиться от избыточной информации, мы можем выполнить округление и преобразование в целочисленный тип или посчитать, сколько чисел попадает в тот или иной диапазон.
import numpy as np import matplotlib.pyplot as plt a = np.random.normal(size=1000, scale=2, loc=100) a = a.round().astype('i2') unique, counts = np.unique(a, return_counts=True) for u, c in zip(unique, counts): print(u, 'встречается', c, 'раз') plt.plot(unique, counts) plt.show()
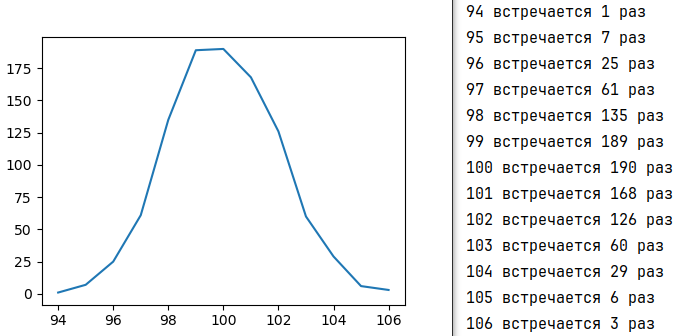
Библиотека Seaborn выполняет многие из этих операций самостоятельно. Поэтому для визуализации непрерывных распределений обычно используют ее. (Однако если строится гистограмма на базе дискретных данных, то достаточно функции hist из Matplotlib, см. следующий урок.)
import numpy as np import matplotlib.pyplot as plt import seaborn as sns a = np.random.normal(size=1000, scale=2, loc=100) sns.displot(a) sns.displot(a, kind='kde') sns.displot(a, kde=True) sns.displot(data=a, kind='ecdf') plt.show()
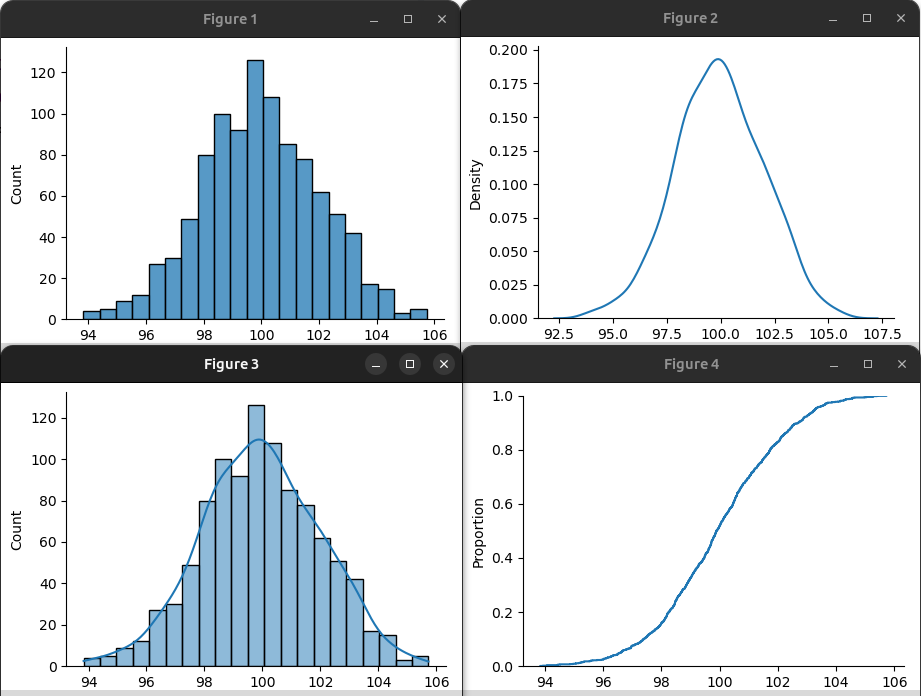
Кроме нормального распределения библиотека NumPy позволяет получить около десятка других. Кратко рассмотрим некоторые из них.
Когда все значения встречаются с одинаковой вероятностью, речь идет о равномерном распределении. С таким мы имеем дело, когда используем генератор случайных чисел языка программирования.
a = np.random.uniform(size=1000) b = np.random.rand(1000) sns.displot(a, kde=True) sns.displot(b, kde=True)
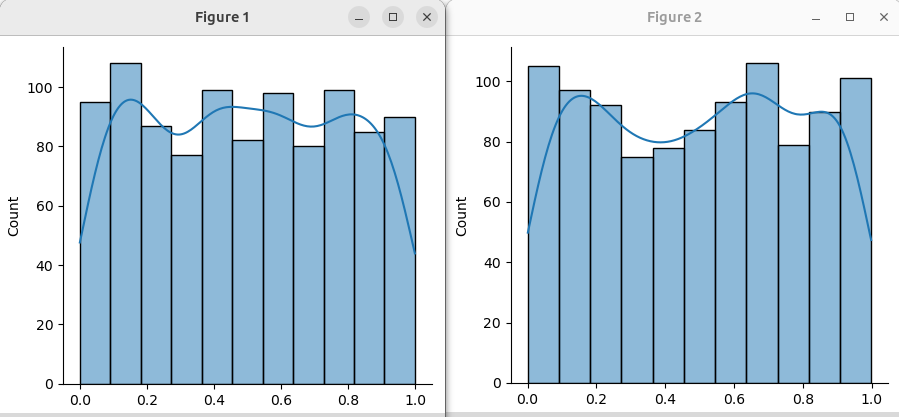
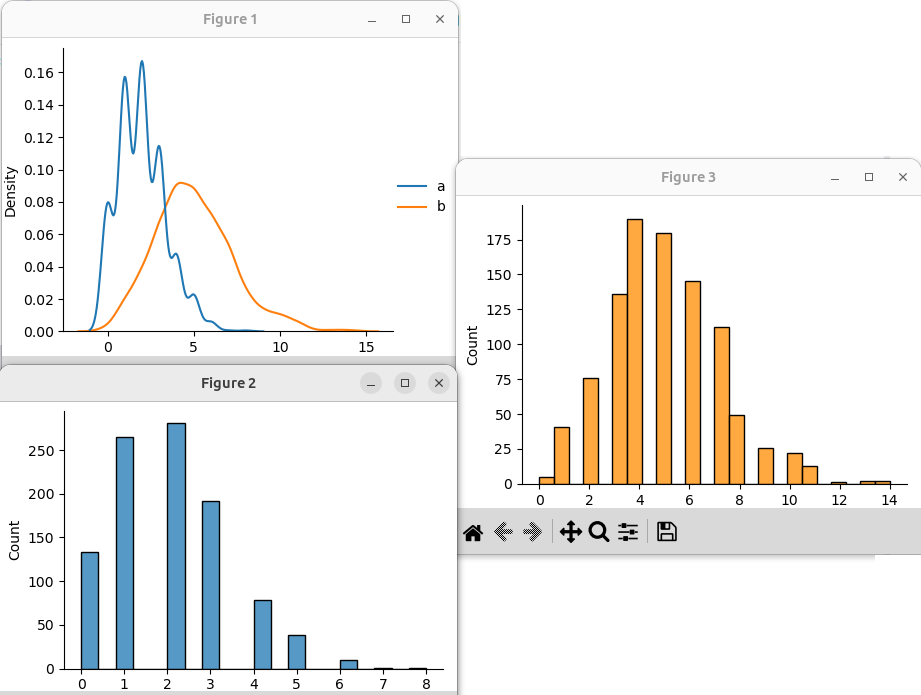
Распределение Пуассона относится к дискретным (в массиве будут только определенные значения) и связано со временем. Оно отражает закономерность, что когда событий в интервале времени происходит определенное количество (в примерах ниже 2 или 5), есть вероятность и иного числа событий. Естественно, эта вероятность (количество таких случаев, значений в массиве) будет уменьшаться с удалением от "центра".
data = { 'a': np.random.poisson(lam=2, size=1000), 'b': np.random.poisson(lam=5, size=1000), } sns.displot(data, kind='kde') sns.displot(data['a']) sns.displot(data['b'], color='darkorange')
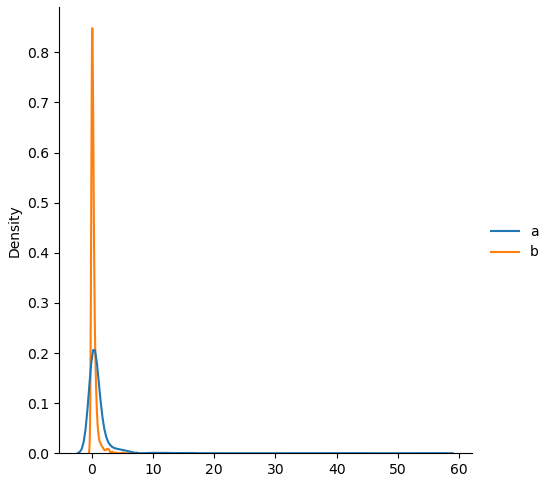
Распределение Парето следует из закона Парето, согласно которому 20% из набора значений дают 80% исхода чего-либо. Параметр a влияет на "хвост" распределений.
data = { 'a': np.random.pareto(a=2, size=1000), 'b': np.random.pareto(a=4, size=1000) } sns.displot(data, kind='kde')
Биномиальное распределение является дискретным. Массив представляет собой отражение количества успешных попыток в каждом эксперименте. В коде ниже в первом случае мы задали восемь экспериментов, в каждом по 10 попыток. Каждая попытка может иметь "успех" или "неудачу". При параметре p = 0.5 вероятность обоих вариантов одинакова. Так только в одном эксперименте было 3 успеха, 4 успеха было в четырех экспериментах, 5 успехов в одном эксперименте и 6 успехов в двух. То есть в данном случае, поскольку количество попыток всего десять, мы можем получить эксперимент, в котором количество успехов достаточно сильно отличаться от 0.5. Понятно, что если попыток будет 100, то количество успехов будет приближаться к 50%. Мы это видим на зеленом графике.
a = np.random.binomial(n=10, p=0.5, size=8) ax = sns.displot(a, color='darkorange') ax.fig.suptitle(f'{a}') plt.xlim((1,10)) b = np.random.binomial(n=100, p=0.5, size=10) sns.displot(b, color='lightgreen') c = np.random.binomial(n=10, p=0.5, size=1000) sns.displot(c) d = np.random.binomial(n=10, p=0.8, size=1000) sns.displot(d, color='c')
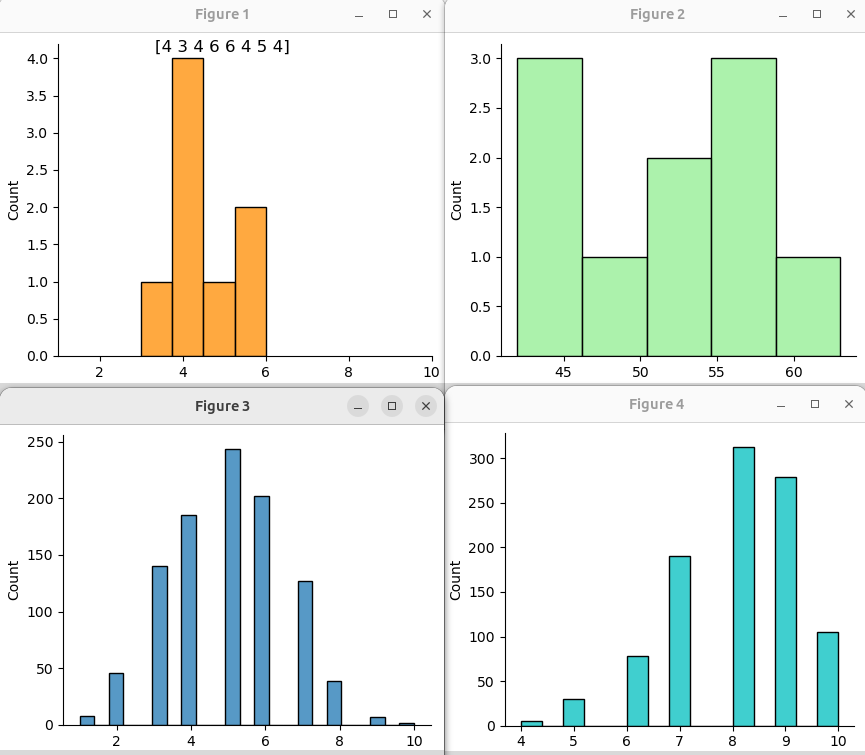
При большом количестве экспериментов с небольшим количеством попыток в каждом график будет иметь вид похожий на нормальное распределение. В примере в последнем массиве вероятность успехов составляет 80%. Мы видим, что экспериментов, где неудач 4 из 10 очень мало. Случаев 3 из 10 вообще нет.