Нормализация массивов NumPy для графиков Matplotlib

Создано: 08.12.2025

Термин "нормализация" используют в разных областях, при этом в статистике под ней понимают действия, направленные на согласование отдельных наборов данных для облегчения их сравнения, то есть данные разного типа становятся подобными друг другу, сопоставимыми. У нормализованных данных отсутствуют единицы измерения. На практике это означает изменение масштаба реальных числовых значений, приведением их диапазону от 0 до 1. Дополнительными преимуществами нормализации являются снижение избыточности и сложности, ясность и получение более качественных данных.

В Python есть библиотеки (scikit-lean, связанная с машинным обучением, и другие), в которых имеются специально предназначенные для нормализации данных функции. Однако в связке NumPy и Matplotlib, когда сопоставимость данных необходима только лишь, например, для применения цветовой карты, можно просто использовать формулы различных способов нормализации.

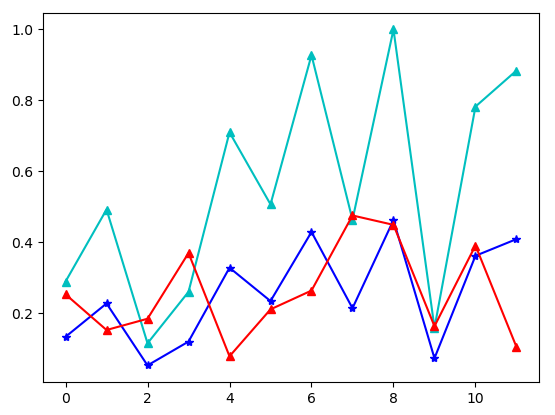
Рассмотрим пример, в котором воксели должны выводиться разным цветом в зависимости от значения элементов в массиве:

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
bx = fig.add_subplot(projection='3d')

b = np.array([[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10],
               [10, 9, 8, 7, 6], [5, 4, 3, 2, 10]],
              [[0, 1, 3, 2, 4], [3, 6, 7, 8, 9],
               [5, 7, 3, 8, 1], [1, 3, 5, 7, 2]]])

bx.voxels(b, edgecolors='#678',
          facecolors=plt.cm.plasma_r(b/np.max(b)))
bx.set_xticks([0, 1, 2])
bx.set_xlabel('X'); bx.set_ylabel('Y'); bx.set_zlabel('Z')

plt.show()

Здесь мы сопоставляем числа в массиве цветам по шкале "плазма реверс", которая градуирована в долях единицы. Чтобы подобное было возможно, требуется получить из исходного массива его нормализованный вид, где значения также будут выражены в долях единицы. В примере выше используется метод нормализации под названием "минимальное-максимальное масштабирование". В полном варианте код выглядел бы так:

l = np.min(b)
h = np.max(b)
scale = np.array([(x - l) / (h - l) for x in b])

bx.voxels(b, edgecolors='#678', facecolors=plt.cm.plasma_r(scale))

Однако если минимумом является ноль, то формула нормализации каждого значения массива сокращается до x / h. В случае поэлементных операций с целым массивом в NumPy это выглядит как b/np.max(b).

Другой простой способ нормализации — метод извлечения остатков (residual extraction), когда из каждого значения массива вычитается среднее значение элементов этого массива. Обычно такой подход используют для сравнения данных со схожими диапазонами.

fig, axs = plt.subplots(1, 2, figsize=(10, 4))

a = np.array([20, 34, 8, 18, 49, 35, 64, 32, 69, 11, 54, 61])
b = np.array([48, 29, 35, 70, 15, 40, 50, 90, 85, 31, 74, 20])

axs[0].plot(a, '*-c')
axs[0].plot(b, '^-y')
axs[0].plot(np.arange(0, len(a)), np.full(len(a), np.mean(a)),
            '--c', alpha=0.5)  # линия среднего значения
axs[0].plot(np.arange(0, len(b)), np.full(len(b), np.mean(b)),
            '--y', alpha=0.5)
axs[0].set_title('Исходные данные')

ar = a - int(np.mean(a))
print(ar)
br = b - int(np.mean(b))
print(br)

axs[1].plot(ar, '*-c')
axs[1].plot(br, '^-y')
axs[1].set_title('Нормализованные данные')

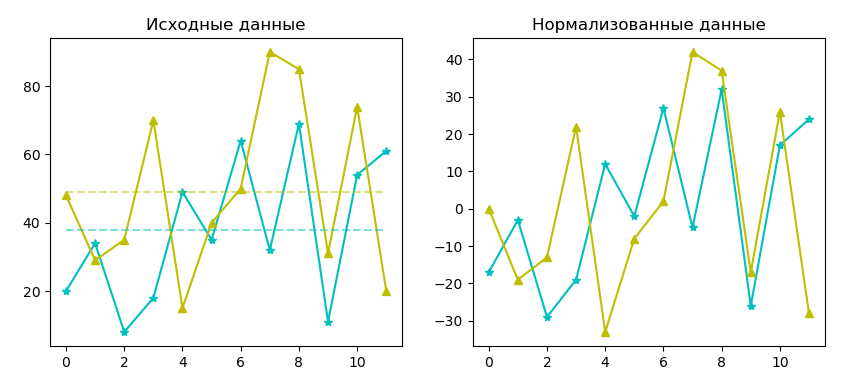
По первому плоту с графиками самих массивов сложнее сказать в каких данных выше дисперсия (больше разброс от среднего значения). На втором, где массивы нормализованы, видно, что от нуля (среднего значения для обоих массивов данных) дальше отклоняются остатки второго.

Подмодуль linalg (linear algebra) библиотеки NumPy содержит различные функции для линейных алгебраических вычислений, среди которых есть функция norm. Она возвращает так называемую норму вектора (одномерного массива) или матрицы (двумерного массива).

Норма — это скалярное положительное значение, характеризующее "размер" массива. Она может вычисляться по-разному. Как именно, указывается через параметр ord (для векторов и матриц набор возможных значений отличается). По-умолчанию для одномерных массивов норма вычисляется по форме L2 (евклидова норма, единичный вектор).

a = np.array([20, 34, 8, 18, 49, 35, 64, 32, 69, 11, 54, 61])
b = np.array([48, 29, 35, 70, 15, 40, 50, 90, 85, 31, 74, 20])
an = np.linalg.norm(a)
an2 = np.linalg.norm(a, ord=np.inf)
bn = np.linalg.norm(b)

plt.plot(a/an, '*-b')
plt.plot(a/an2, '^-c')
plt.plot(b/bn, '^-r')