Box plots — диаграммы размаха в Matplotlib

Создано: 24.12.2025

Диаграммы размаха, или "ящики с усами", позволяют представить распределения вероятностей в компактном виде путем визуализации их основных характеристик: медианы, квартилей, минимума и максимума, выбросов (что они значат, описано ниже). Рассмотрим усиковую диаграмму в сравнении с гистограммой на примере нормального распределения. В модуле pyplot библиотеки Matplotlib коробчатые диаграммы строятся с помощью функции/метода boxplot.

import numpy as np
import matplotlib.pyplot as plt

a = np.random.normal(50, 3, 500)

fig, axs = plt.subplots(2, 1, figsize=(6, 8))

axs[0].hist(a, bins=20, rwidth=0.95)

axs[1].boxplot(a, vert=0, labels='a')  # параметры зависят от версии
axs[1].grid(axis='x')

plt.show()

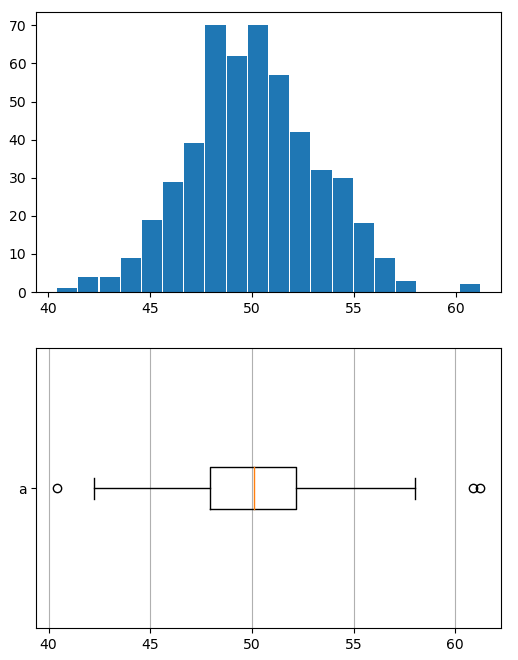
По умолчанию боксплоты выводятся вертикально, мы положили его горизонтально, чтобы было легче сравнивать с гистограммой. Представьте, что полученный с помощью NumPy массив a был неявно упорядочен по возрастанию. Оранжевая линия внутри ящика — это медиана. Ее не надо путать с арифметически средним, медиана — это срединное значение. Медиана определяется через упорядочение массива. Ей будет являться число, которое находится в центре такового. Если элементов в массиве четное количество, то два стоящих в середине складываются и делятся на два (по-сути находится среднее двух медиан).

Медиана одновременно является 0,5-м квартилем (или 50%-м процентилем). Квартили делят упорядоченный массив на четыре равные части. На диаграмме размаха сам ящик (коробка, блок) формируется между 0,25-м до 0,75-м квартилями и его размер обозначает диапазон значений, которые укладываются в эти "примедиальные" квартили (межквартильный размах). Если ящик маленький, это говорит о том, что в массиве есть много чисел с близкими к медиане значениями. Их количества достаточно, чтобы занять все места массива, отводимые для срединных квартилей.

Если выбросы отсутствуют, то черточки на концах усов обозначают минимальное и максимальное значения в массиве. В его упорядоченной версии это будут значения первого и последнего элемента.

Чтобы определить, если ли выбросы по обе стороны, из значения начала первого квартиля (0,25-й) вычитают полуторную величину межквартильного интервала, а к началу третьего квартиля (0,75-й) добавляют полуторную величину межквартильного размаха. Полученные значения определяют длину усов боксплота, их концы — края статистически значимой выборки. Если есть значения, выходящие за концы, значит есть выбросы.

     Q1-1.5IQR   Q1  медиана  Q3   Q3+1.5IQR
                  |-----:-----|
  o      |--------|     :     |--------|    o  o
                  |-----:-----|
выброс            <----------->           выбросы
                       IQR

Расстояния между различными частями ящика позволяют определить степень дисперсии и асимметрии данных.

С помощью параметров notch (наличие выемок) и bootstrap (рекомендуемые значения от 1000 до 10000) можно отображать в виде зарубок и указывать так называемый доверительный интервал (см. последний пример этого урока).

Помимо того, что умение интерпретировать диаграммы размаха позволяет одним взглядом оценивать сами распределения, "ящики с усами" удобны для сравнения их между собой (пример ниже взят из справки по Matplotlib).

np.random.seed(19680801)
fruit_weights = (
    np.random.normal(130, 10, size=100),
    np.random.normal(125, 20, size=100),
    np.random.normal(120, 30, size=100)
)
labels = ['peaches', 'oranges', 'tomatoes']
colors = ['peachpuff', 'orange', 'tomato']

fig, ax = plt.subplots()
ax.set_ylabel('fruit weight (g)')

bplot = ax.boxplot(fruit_weights, patch_artist=True, labels=labels)

for patch, color in zip(bplot['boxes'], colors):
    patch.set_facecolor(color)

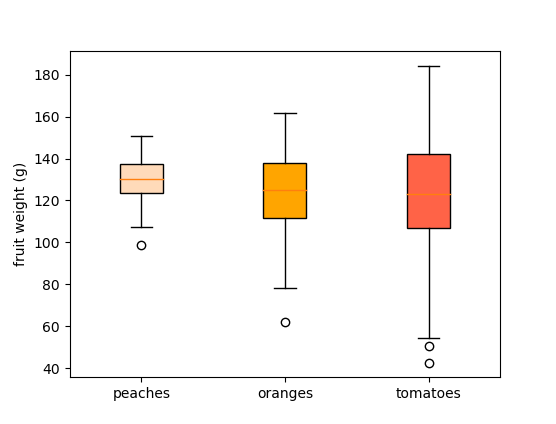
Наиболее выраженные отличия можно увидеть, сравнивая боксплоты разных распределений:

data = (
    np.random.uniform(80, 120, size=100),
    np.random.normal(100, 10, size=100),
    np.random.pareto(size=100, a=10) * 200,
    np.random.binomial(size=100, n=10, p=0.8) * 10,
)

plt.boxplot(data, patch_artist=True,
            labels=('uniform', 'normal', 'pareto', 'binomial'))
plt.ylabel('Values')

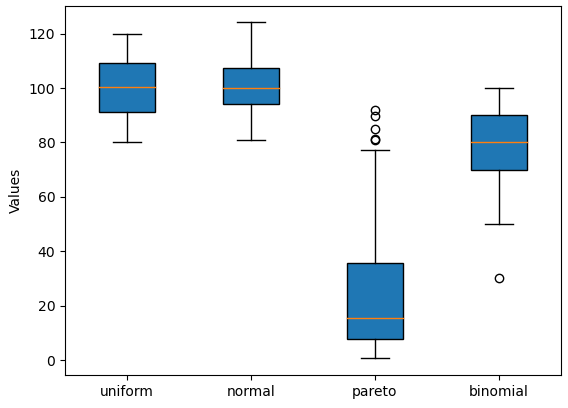
Кроме медианы, boxplot() позволяет обозначать на диаграмме среднее значение. Для этого используется параметр showmeans.

plt.boxplot(data, showmeans=True, meanline=True, notch=True,
            labels=('uniform', 'normal', 'pareto', 'binomial'))

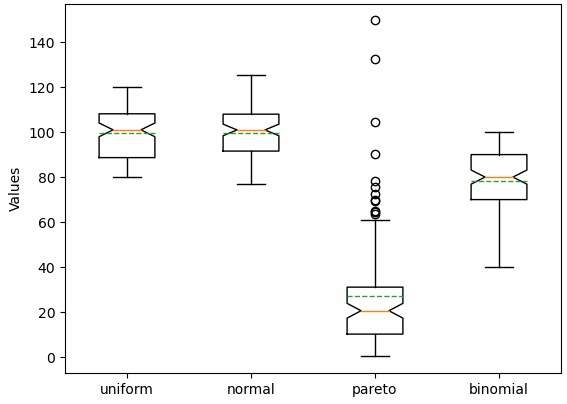
Получить сами данные можно с помощью модуля cbook:

import matplotlib.cbook as cbook

a = np.random.normal(50, 3, 500)
plt.boxplot(a)

stats = cbook.boxplot_stats(a)
for i in stats[0]:
    print(i, stats[0][i])

mean 49.91551182353907
iqr 3.9511495739328666
cilo 49.534831196709234
cihi 50.08967164820666
whishi 57.55879344804599
whislo 42.7640992450584
fliers [41.83158929 38.73954884 59.32456169 58.43105926 58.2007655 ]
q1 47.8876446243917
med 49.81225142245795
q3 51.838794198324564

Также в NumPy есть свои функции для квартилей, процентилей, медианы и др.