Матрицы и вложенные циклы в Python

В программировании циклы можно вкладывать друг в друга. Причем комбинации могут быть какими угодно. В наиболее простом случае внешний цикл содержит один внутренний.

Необходимость во вложении циклов бывает разная. Один из примеров ‒ формирование матриц.

В программировании матрицами обычно называют двумерные массивы. Двумерные – значит, каждый элемент массива сам представляет собой массив. Эти вложенные массивы обычно одномерные, иначе придется говорить о трехмерных или многомерных матрицах.

При этом все вложенные массивы должны иметь одинаковую друг с другом длину, потому что матрицу обычно представляют в виде правильного прямоугольника, то есть привычной двумерной таблицы, в которой все строки равны между собой по длине.

Размерность таблицы, измеряется количеством строк и столбцов. В переводе на язык матриц количество строк – это количество вложенных массивов, количество столбцов – это количество элементов в одном вложенном массиве.

Поскольку в Python нет встроенного в язык типа данных "массив", а есть во многом похожий "список", то и матрицы будем строить из списка. Пусть нам нужна матрица 3x4 из случайных чисел. Программа ее генерации и вывода на экран может выглядеть так:

from random import randint
N = 3
M = 4
a = []

for i in range(N):
    b = []
    for j in range(M):
        b.append(randint(1,99))
    a.append(b)

print(a, end='\n\n')

for i in range(N):
    for j in range(M):
        print('%3d' % a[i][j], end='')
    print()

Результат:

[[38, 21, 71, 71], [7, 68, 74, 72], [23, 98, 60, 44]]

 38 21 71 71
  7 68 74 72
 23 98 60 44

Сначала мы выводим матрицу в одну строку только для того, чтобы показать, как данные хранятся в списке.

Обращение к элементам матрицы происходит через их индексы. Сначала указывается номер строки, затем номер столбца. Так, чтобы в примере выше извлечь число 7, надо написать выражение a[1][0], потому что число 7 находится во второй строке, чей индекс 1, и в первом столбце, чей индекс 0.

В Python из-за возможностей цикла for не обязательно пользоваться индексами при выполнении перебора. Цикл вывода на экран может выглядеть и так:

for i in a:
    for j in i:
        print("%3d" % j, end="")
    print()

Здесь мы извлекаем сначала очередной список из a. После перебираем этот вложенный список во вложенном цикле.

Для получения матрицы можно использовать списочные выражения:

a = [[randint(1,99) for j in range(M)] for i in range(N)]

Здесь одно списочное выражение вложено в другое. Вложенное выполняется N раз, и на каждом создается отдельный список. С другой стороны, часто генераторы списков с двойным for выглядят так:

matrix = [[10, 21, 30], [3, 4, 9]]
odd = [item for row in matrix for item in row if item%2 != 0]
print(odd)

a = [i * j for i in range(1, 4) for j in range(1, 5)]
print(a)

Результатом их выполнения будут одномерные списки:

[21, 3, 9]
[1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12]

Последний пример мы можем переписать обычными циклами, один из которых вложен в другой, и получить таблицу умножения:

for i in range(1, 7):
    for j in range(1, 10):
        print(f'{i*j:4}', end='')
    print()

Результат:

   1   2   3   4   5   6   7   8   9
   2   4   6   8  10  12  14  16  18
   3   6   9  12  15  18  21  24  27
   4   8  12  16  20  24  28  32  36
   5  10  15  20  25  30  35  40  45
   6  12  18  24  30  36  42  48  54

При изучении программирования, когда дело доходит до матриц, то рассматривается множество задач: на нахождение определенных элементов, вычисление сумм, сортировку и тому подобное. В основном эти задачи связаны с перебором элементов то так, то этак. В Python многое упрощается в связи с наличием встроенных функций и методов. Хотя никто не мешает использовать и изучать классические алгоритмы.

В квадратных матрицах (у таких количество строк равно количеству столбцов) выделяют диагонали. Главная диагональ идет от верхнего левого угла к нижнему правому. Побочная диагональ – от верхнего правого к нижнему левому. Первый и второй индекс любого элемента главной диагонали одинаковые. Так первый элемент [0][0], второй [1][1].

Индексы каждого элемента побочной диагонали в сумме должны давать размерность матрицы за минус 1 (если индексация идет с нуля).

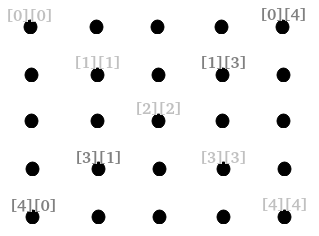
Вычисление суммы элементов каждой диагонали выполняется без вложенных циклов:

from random import randint
N = 5

# заполняем и сразу выводим
a = []
for i in range(N):
    b = []
    for j in range(N):
        n = randint(1, 9)
        b.append(n)
        print('%3d' % n, end='')
    a.append(b)
    print()

# находим сумму элементов главной и побочной диагоналей
diagonal1 = 0
diagonal2 = 0
for i in range(N):
    diagonal1 += a[i][i]
    diagonal2 += a[i][N-1-i]

print(diagonal1)
print(diagonal2)

Пример выполнения:

  6  8  9  5  5
  7  1  5  3  8
  1  5  4  4  8
  6  9  5  3  4
  2  2  7  7  1
15
23

Практическая работа

Заполните матрицу случайными положительными и отрицательными числами. Выведите ее на экран так, чтобы вместо отрицательных чисел стояли прочерки, например:
```
  2  -  5  6
  -  0  -  -
  5  4  -  -
```
Найдите сумму элементов каждого столбца матрицы.

Примеры решения и дополнительные уроки в pdf-версии курса