Битовые операции в языке Си. Восьмеричные и шестнадцатеричные числа

Данный урок курса можно считать факультативным, т. е. необязательным. Для освоения темы этого урока вам потребуется знание о двоичной системе счисления, навыки перевода чисел из одной системы счисления в другую, а также вы должны иметь представление о том, что такое битовые (они же поразрядные) операции. С последним можно познакомиться по вот этой лекции.

В языке программирования C существуют следующие поразрядные операции: & (И), | (ИЛИ), ^ (исключающее ИЛИ), << (сдвиг влево), >> (сдвиг вправо), ~ (поразрядное дополнение до единицы). Рассмотрим на примерах, как они работают, но перед этим уделим внимание выводу чисел в отличных от десятичной системах счисления.

В C можно присваивать целочисленные значения в десятичной, восьмеричной и шестнадцатеричной системах счисления. Для того, чтобы присвоить переменной число в восьмеричной системе счисления, перед ним надо написать 0 (ноль), в шестнадцатеричной — 0x (ноль и икс), например:

int a, b;
a = 077; // восьмеричное число
b = 0x1F; // шестнадцатеричное число

Любые целые числа можно выводить на экран в десятичном, восьмеричном и шестнадцатеричном представлении. Пример кода для вывода определенных ранее двух переменных в различных системаъ счисления:

printf("%d %o %x %X\n", a, a, a, a);
printf("%d %o %x %X\n", b, b, b, b);

В результате на экране вы увидите:

63 77 3f 3F
31 37 1f 1F

Восьмеричные и шестнадцатеричные числа используются из-за удобства при работе с двоичной системой счисления. Каждая цифра восьмеричного числа может быть заменена тремя цифрами двоичного. И каждая цифра шестнадцатеричного числа легко заменяет четыре разряда двоичного числа. Вот таблица соответствия цифр восьмеричной системы счисления числам двоичной системы:

0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Теперь допустим, что у нас есть восьмеричное число 037. По таблице легко понять, что в двоичном выражении оно будет выглядеть как 011 111.

Шестнадцатеричное число 7D в двоичной системе счисления будет выглядеть как 0111 1101.

Если бы мы при работе с поразрядными операциями использовали десятичные числа, то чтобы оценить результат нам бы каждый раз приходилось переводить десятичное число в двоичную систему счисления, что относительно трудоемко. Если же человек видит, например, восьмеричное число, то он может представить как оно выглядит в двоичном представлении, помня или держа перед глазами таблицу соответствия чисел. Например, как только мы видим 017, то можем представить в уме, как последние четыре бита ячейки памяти забиты единицами.

Теперь вернемся к поразрядным операциям и посмотрим как работает каждая из них. Для этого напишем небольшую программу:

int a, b;
a = 017;
b = 036;
printf("0%o & 0%o = 0%o\n", a, b, a & b);
printf("0%o | 0%o = 0%o\n", a, b, a | b);
printf("0%o ^ 0%o = 0%o\n", a, b, a ^ b);
printf("0%o << 2 = 0%o\n", a, a << 2);
printf("0%o >> 2 = 0%o\n", a, a >> 2);
printf("~0%o = 0%o\n", a, ~a);

Результат ее работы будет выглядеть так:

017 & 036 = 016
017 | 036 = 037
017 ^ 036 = 021
017 << 2 = 074
017 >> 2 = 03
~017 = 037777777760

Этот результат будет проще понять с помощью рисунка:

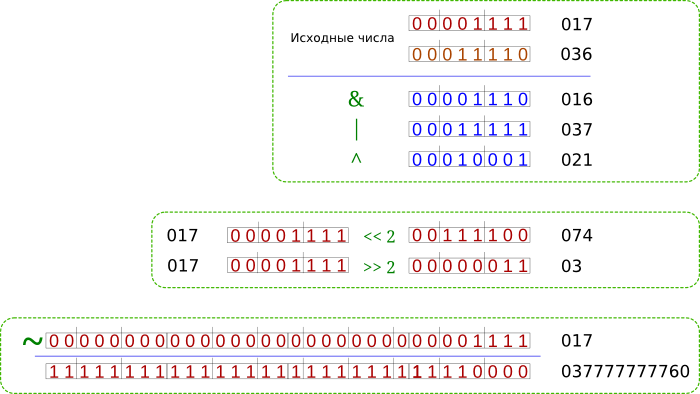
В последнем случае получилось такое большое число потому, что под форматы вывода целых чисел (%d, %o, %X) выделяется по 4 байта.

Теперь рассмотрим пример использования битовых операций. Допустим, у нас есть массив, требуется снять с него "маску", которая бы отражала, в какой позиции стоят отрицательные, а в какой положительные элементы. Пусть единица в бите обозначает соответствующий ей положительный элемент массива, а ноль — отрицательный. Так "битовая маска" массива {4, -3, 2, 2, 8, -1} будет выглядеть как 101110, или в восьмеричном представлении как 056. Составим алгоритм решения этой задачи:

Будем считать, что массив состоит не более чем из 32 элементов. Поэтому для хранения его "маски" достаточно переменной типа int. Назовем ее mask и присвоим значение 0.
Переберем элементы массива в цикле for. Если встречается положительный элемент, то установим соответствующий ему бит значения mask в 1.
Выведем значение переменной mask на экран в виде восьмеричного числа.

Вроде бы все просто, но как установить в единицу определенный бит числа? Существует закономерность соответствия степеней двойки и двоичного представления числа:
2⁰ = 0000 0001
2¹ = 0000 0010
2² = 0000 0100
2³ = 0000 1000
2⁴ = 0001 0000
и т.д. Теперь если применить к mask побитовую операцию | (ИЛИ), а в качестве второго операнда использовать определенную степень двойки, то один бит будет установлен в 1. Например:
(0) 0000 0000 | (2⁵) 0010 0000 = 0010 0000
(32) 0010 0000 | (2⁷) 1000 0000 = 1010 0000

При переборе первый элемент массива имеет индекс 0, но соответствующий ему бит в maskдолжен стоять впереди остальных. Если известно общее количество элементов массива (N), то можно определить степень двойки по формуле N - i - 1. Так, имея четвертый положительный элемент массива (его индекс 3) из 10 элементов, следует установить в единицу седьмой с конца бит (он же будет четвертым с начала), а это значит надо использовать вторым операндом битового ИЛИ 2⁶, а 6 как раз будет 10(N) - 3(i) - 1.

Другая проблема — как в языке C возвести число в степень. Понятно, что можно написать свой код, но скорее всего в стандартной библиотеке уже есть подобная функция. С помощью заголовочного файла math.h можно подключить библиотеку с математическими функциями. Среди них есть функция pow(), которая принимает два числа и возвращает результат возведения первого числа в степень, выраженную вторым числом. Однако результат возвращается в виде вещественного числа, а нам требуется целое. Как быть? В Си есть операции приведения типов, которые меняют тип значения с одного на другой. Например, чтобы преобразовать значение вещественной переменной a в целое, следует написать (int) a.

Вот как может выглядеть вышеописанная программа:

#include <stdio.h>
#include <math.h>
 
#define N 12
 
int main() {
    int nums[N] = {7, 3, 9, -5, -3, 2,
                   1, 0, 16, -4, 2, 0};
    int mask = 0;
 
    for (int i = 0; i < N; i++)
        if (nums[i] >= 0)
            mask = mask | (int) pow(2, N-i-1);
 
    printf("%o\n", mask);
}

Если у вас не получается скомпилировать программу, добавьте в конце вызова gcc опцию -lm (например, gcc -o bits bits.c -lm).

Курс с решением задач:
pdf-версия